Veri Yapısında Ağaç Nedir ve Nasıl Gezinir?
Veri Yapısında Ağaç
Ağaç Geçişi, Çeşitli Yazılımlarda En Yaygın Olarak Kullanılan Algoritmalardan Biridir. Ağaç, hiyerarşik olarak ilişkili olan köşelerden ve kenarlardan oluşan bir veri yapısıdır.
Ağaç geçişinde, ağacın tüm köşelerine sıralı bir şekilde erişmek için bir algoritma vardır.
Veri yapısındaki ağaç nedir?
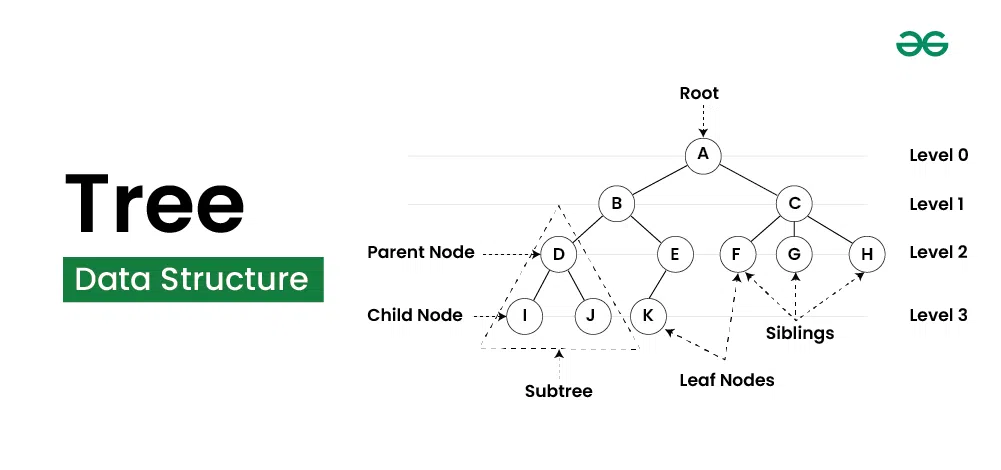
Bir veri yapısındaki bir ağaç, kök dışında her köşenin bir ebeveyni ve bir veya daha fazla çocuğu olan, hiyerarşik bir biçimde bir köşeler ve kenarlar kümesidir. Veri yapısındaki bir ağaç, bir kök tepe noktası ve yönlendirilmiş kenarlardan oluşan belirli bir grafik türüdür. Veri yapısındaki ağaç aşağıdaki gibi temsil edilebilir:
O
/ | \
o o o
/ \ |
o o o
Bu ağaçta, birincil köşe köktür ve diğer köşeler hiyerarşik olarak onun altındadır. Her köşe noktası birden çok çocuğa bağlanabilir, ancak her çocuk yalnızca bir ebeveyne bağlanır.
Veri yapısında bir ağaç, arama, sıralama, veri dönüştürme vb. değişiklikler ve metin verilerini analiz etmek ve ayrıştırmak için bir ayrıştırma ağacı.
Ağaç gezintisi
Ağaç geçişinde, ağaç düğümleri belirli bir sırayla ziyaret edilir. Bu gezinme derin veya yüzeysel olabilir. Derinlemesine geçiş, önce bir kök tepe noktası seçilir, ardından derinlemesine, mevcut tepe noktasının alt öğelerinin her biri yeni bir tepe noktası olarak seçilir ve çapraz geçiş, bir dizi köşeye ulaşmaya devam eder. Yüzey geçişinde, ağaç köşeleri farklı seviyelerde sırayla ziyaret edilir.
Ağaç seviyesi, birçok bilgisayar yazılımında bir veri yapısı olarak kullanılır. Örneğin, ikili arama algoritmalarında ve optimum çözüm optimizasyonu problemlerini bulmada ağaçlar kullanılır. Ayrıca problemstraveratheistheis grafik ve oyun geliştirme yazılımlarında kullanılan yazılımlarda grafik nesneleri gösterir.
Ağaç gezinme türleri nelerdir?
En önemlileri aşağıdaki gibi farklı ağaç gezintisi türleri vardır:
Derinlik öncelikli arama
Derinlik-Önce Arama, başlangıç tepe noktası olarak bir tepe noktasının seçildiği ağaç geçiş yöntemlerinden biridir ve en fr her kenar, bu yöntemde tüm alt tepe çocukları, önce bir tepe noktasına gideriz ve sonra tüm alt köşelere geri döneriz. bir dizi köşeye ulaşana kadar bu köşenin çocukları vb.
Ağaç geçişi, özyinelemeli ve yığın tabanlı olmak üzere iki türe ayrılır. Özyinelemeli yöntemde, geçiş özyinelemeli işlev kullanılarak gerçekleştirilir ve her adımda, geçerli tepe noktasının çocukları sırayla ziyaret edilir. Yığın yönteminde, köşeleri depolamak için bir yığın kullanılır ve her adımda, geçerli köşe yığının üzerine yerleştirilir ve ardından tüm alt öğeleri yığına sırayla eklenir.
Ağaç yapısına göre, önce derinlik araması, önce en iyi ile derinlik öncelikli arama olarak da gerçekleştirilebilir. Bu yöntemde, her köşe ziyaret edilmeden önce, kalitesini değerlendirmek için bir fonksiyon tanımlanır ve i. İntep, en iyi değerlendirmeye sahip tepe noktası bir sonraki tepe noktası olarak seçilir.
Derinlik öncelikli ağaç geçişi, düğümde derinlik öncelikli arama ve ilk sayfa arama problemleri gibi birçok problemde kullanılır.
Genişlik Öncelikli Arama
Breadth-First Search ağaç geçişi, önce kökü seçtiğimiz, ardından mevcut düzeydeki tüm köşelerin ilk alt öğelerini sırayla ziyaret ettiğimiz ve ardından bir sonraki düzeye geçtiğimiz ağaç geçişi yöntemlerinden biridir. Başka bir deyişle, bu yöntemde önce başlangıç köşesinin tüm çocuklarını, sonra tüm çocuklarını vb.
Ağaç geçişi, yüzeysel olarak kuyruk (kuyruk tabanlı) ve çift uçlu (çift uçlu) türlere ayrılır. Kuyruk yönteminde, köşeleri saklamak için bir satır kullanılır ve her adımda, mevcut köşe satırdan kaldırılır ve tüm alt öğeleri çubuğa eklenir. Çift yönlü yöntemde, köşeleri saklamak için çift yönlü bir sütun kullanılır ve her adımda çizginin her iki tarafındaki köşeler sırayla ziyaret edilir.
Ağaç geçişi genellikle iki köşe arasındaki en kısa yolu aramak, en az maliyetli yolu bulmak, grafiksel problemler ve benzeri problemler için kullanılır. Ayrıca, optimum sonuca ulaşmak için birçok konuda derinlik ve yüzey navigasyonuna ihtiyaç duyulabilir.
Sipariş Sonrası Geçiş
Postorder traversal, traversalın bir tepe noktasının çocuklarından başladığı ağaç traversal yöntemlerinden biridir. Geçerli tepe noktasına dönüyoruz, ardından ana tepe noktasına ve ardından ebeveynin solundaki veya sağındaki başka bir tepe noktasına gidiyoruz. Başka bir deyişle, bu yöntemde önce bir tepenin tüm çocukları, sonra tepenin kendisi ziyaret edilir.
Postorder traversal‘da önce mevcut köşenin tüm sol çocuklarını, sonra tüm sağ çocuklarını ziyaret ederiz ve son olarak mevcut köşenin kendisini görürüz. Bu yöntem, bir ağaç ifadesinin değerini hesaplamak, bir ağacın yüksekliğini hesaplamak veya bir ağacın derinliğini hesaplamak için çok uygundur.
Sipariş sonrası geçiş, ağaç geçişinin standart yöntemlerinden biridir. Bir Boole ifadesinin değerini hesaplama algoritması, bir ağaç köşesinin derinliğini hesaplama algoritması ve bir ağaçtaki yaprak sayısını bulma algoritması gibi birçok ağaç işleme algoritmasında kullanılır.
Ön Sipariş Geçişi
Ön sipariş geçişi, geçişin kökten başladığı ve ardından bir tepe noktasının solunu ve sağını ziyaret ettiği ağaç geçiş yöntemlerinden biridir. Başka bir deyişle, bu yöntemde önce mevcut tepe noktasını, sonra tüm sol çocuklarını ve sonra tüm sağ çocuklarını görüyoruz.
Daha doğrusu, preorder traversal’da önce mevcut vertex’i, sonra l onun sol çocuklarını ve sonra sağ çocukları aracılığıyla ziyaret ederiz. Bu yöntem, bir ağacın bir kopyasını oluşturmak, iki köşe arasında bir ağaç yolu bulmak veya bir ağaçtan sonek ifadesi oluşturmak için iyi çalışır.
Ön sipariş geçişi, standart ağaç geçişi yöntemlerinden biridir. Minimum kapsayan ağaç algoritması, ikili arama ağacı algoritması ve bir ağaç ifadesinin değerini hesaplama algoritması gibi birçok ağaç işleme algoritmasında kullanılır.
Sıralı Geçiş
Sıralı geçiş, geçişin sırayla sol çocukları, geçerli tepe noktasını ve ardından bir tepe noktasının sağ çocuklarını ziyaret ettiği ağaç çaprazlama yöntemlerinden biridir. Başka bir deyişle, bu yöntemde önce mevcut köşenin tüm sol çocuklarını, sonra köşenin kendisini ve sonra tüm sağ çocuklarını ziyaret ederiz.
Sıralar arası geçişte, önce mevcut köşenin tüm sol çocuklarını ziyaret ederiz, ardından mevcut köşeyi ve tüm sağ çocuklarını görürüz. Bu yöntem, bir ağaçtaki öğeleri sıralamak, bir ağaçtan bir ek ifadesi oluşturmak veya bir ağaçtaki en büyük ve en küçük köşelerin değerini bulmak için iyi çalışır.
Sıralar arası geçiş, ağacı çaprazlamanın standart yöntemlerinden biridir. İkili arama ağacı oluşturma algoritması, bir ağaç ifadesinin değerini hesaplama algoritması ve bir ağaç tepe noktasının derinliğini hesaplama algoritması gibi birçok ağaç işleme algoritmasında kullanılır.
Başka hangi ağaç geçiş algoritmaları var?
Sıra öncesi geçiş, orta sıra geçiş ve sıra sonrası geçişe ek olarak, ağaç geçişi için genellikle iki kategoriye ayrılan başka algoritmalar da vardır: genişlik öncelikli geçiş ve derinlik öncelikli geçiş. Aşağıda bu algoritmalardan bazıları verilmiştir:
- Seviye-Sıra Geçişi: Bu algoritma kökten başlar ve her seviyenin köşeleri sırayla geçilir, ardından bir sonraki seviye adreslenir.
- Derinlik-Önce Arama (DFS): Bu algoritmada kökten başlar ve bir tepenin tüm çocukları taranır, ardından tüm köşeler kontrol edilene kadar bir sonraki tepe adreslenir.
- Derinlik-Önce Geçiş – Önce Sol: Bu algoritma, her adımda bir tepe noktasının ilk sol alt öğesinin geçilmesi dışında DFS algoritmasına benzer.
- Derinlik-Önce Geçiş – Önce Sağ: Bu algoritma, her adımda bir köşenin ilk sağ alt öğesinin geçilmesi farkıyla DFS algoritmasına benzer.
- Çift Ön Sıra Geçişi: Bu algoritmada, bir tepe noktasının sol çocukları geçilir, ardından tepe noktası ve onun tüm sağ çocukları geçilir.
- Çift Sıralı Geçiş: Bu algoritmada, bir tepe noktasının sağ çocukları geçilir, ardından tepe noktasının kendisi ve tüm sol çocukları geçilir.
- Çift sıralı geçiş: Bu algoritmada, bir tepe noktasının sağ çocukları geçilir, tüm sol çocukları çaprazlanır ve son olarak tepe noktasının kendisi ziyaret edilir.
Geri dönmeyen ön sipariş geçişi ve geri dönmeyen sıralar arası geçiş gibi diğer teknikler, yığını kullanarak ağacı çaprazlamak için kullanılır. Bu yöntemlerde, bir yığın geri aramalar yerine köşeleri depolar. Bu yöntemle, DFS algoritmalarının tüm avantajlarından yararlanırız ancak vektör uzunluğunda bellek veya kuyruklar kullanmamıza gerek kalmaz.
Genel olarak, ağaç geçişi için kullanılan herhangi bir algoritma, problemin gereksinimlerine ve ağacın özelliklerine göre seçilmelidir.
Genel ağaç nedir?
Genel ağaç, her tepe noktasının birden fazla çocuğu olabileceği bir ağaçtır. Genel bir ağaç, bir köşe ağı gibidir; kök dışındaki her köşenin birkaç çocuğu olabilir.
Genel bir ağaçta, her tepe noktası iki parça içerir: veriler ve alt öğelerinin listesi. Örneğin, bir kitapta, her karakterin bir tepe noktası olduğu ve alt öğelerinin onu takip eden karakterleri içerdiği genel bir karakter ağacı oluşturabilirsiniz.
Genel ağaç, ağaç geçişi ve ağaç yüksekliği hesaplama algoritmaları gibi birçok ağaç işleme algoritmasında kullanılır. Ayrıca, genel ağaç, XML ve HTML gibi veri yapılarını temsil etmek için kullanılabilir.
Sonsuzluk ağacı nedir?
Sonsuz veya lambda ağacı, sınırsız köşeleri ve kenarları olan belirli bir ağaçtır. Bu ağaçta, her köşe sonsuz sayıda başka köşeye bağlanabilir. Sonsuz bir ağaç aşağıdaki gibi temsil edilebilir:
O
|
O
|
O
|
O
…
Bu ağaçta, her köşenin ana köşesine bağlı tek bir kenarı vardır ve hiçbir köşenin ağacın tepesine göre bir avantajı yoktur. Sonsuz bir ağaç, birim kenarları olan sonsuz bir köşeler zinciri olarak temsil edilebilir.
Sonsuz ağaçlar, matematik, fizik, grafik teorisi, programlama ve yapay zeka gibi birçok bilimsel ve endüstriyel problemde kullanılmaktadır. Örneğin sonsuz bir ağaç, sonsuz bir zaman serisini veya sürekli sensör verilerini temsil edebilir. Ayrıca lambda ağaçları, sinir ağları ve Boltzmann makineleri gibi dinamik sistemleri modelleyebilir.
son söz
Her yöntem farklı problemlerde kullanıma uygundur ve bazı durumlarda bu yöntemlerin bir kombinasyonu gerekebilir. Genel olarak ağaç geçişi, birçok problemde kullanılan en kritik veri yapısı algoritmasıdır.