blog posts

Fiyatı analiz etmek ve tahmin etmek için genellikle iki kategorideki verilere ihtiyacımız var:

1. Bir sembolün fiyatı, bir sembolün hacmi veya diğer semboller gibi mikro değişkenler
2. Küresel altın fiyatı , küresel petrol fiyatı, endeksler gibi makro değişkenler

Genel olarak iyi bir tahmin yapmak için çok sayıda mikro değişkene ve çok sayıda makro değişkene sahip olmak faydalıdır. Örneğin, İran borsasındaki bir hisse için doğru bir tahmin yapmak aşağıdaki değişkenleri gerektirebilir :

1. Payın kendisiyle ilgili değişkenler
2. Toplam endeks ve bakiye endeksi
3. Banka faiz oranı
4. Şişirme
5. Altının dünya fiyatı
6. Forex piyasasında (Döviz Piyasası) bazı göstergeler

Öte yandan ” Temel Analiz ” ile ilgili niteliksel verilerin de büyük etkisi olabilir, bunun sayısallaştırılması ve veri setine dahil edilmesi daha iyidir.

“Google Trend” gibi kaynaklardan alınan ve genel popülerliği gösteren bazı veriler de çok yararlı olabilir. Bu nedenle, kullanılan bilgi aralığı ne kadar geniş olursa analiz de o kadar geçerli ve doğru olur. Elbette verilerin son derece güvenilir olması gerektiğini ve ayrıca zaman serisi verilerinde var olan özel düzen nedeniyle verilerin birbiriyle birleştirilip “kaynaştırılabilmesi” (Veri Füzyonu) gerektiğini de belirtmek gerekir .

Python diliyle programlamayı öğrenmek için, bağlantısı aşağıda verilen ileri düzey Python eğitimlerine giriş serisine başvurmanızı öneririz.

Python’da fiyat tahmini

Şimdi Python’da modelleri uygulamak ve fiyat tahmini yapmak için programlama ortamına girip gerekli kütüphaneleri çağırıyoruz:

import numpy as np
import pandas as pd
import datetime as dt
import yfinance as yf
import mplfinance as mplf
import sklearn.metrics as met
import matplotlib.pyplot as plt
import pandas_datareader as pdt
import sklearn.linear_model as lm
import sklearn.preprocessing as pp
import statsmodels.graphics.tsaplots as tsaplt

Bu kütüphaneler sırasıyla aşağıdaki amaçlar için kullanılacaktır:

1. Dizilerle ve vektör hesaplamalarıyla çalışma
2. Veri çerçeveleri ve verilerle çalışma
3. Tarih ve saati kullan
4. Alınan veri
5. Finansal tabloların çizilmesi
6. Model değerlendirme kriterlerinin hesaplanması
7. Grafikler
8. Alınan veri
9. Doğrusal modeller oluşturma ve eğitme
10. Veri ön işleme
11. Zaman serisi analizi grafiklerinin çizilmesi

Şimdi aşağıdaki ayarları uyguluyoruz:

np.random.seed(0)
plt.style.use('ggplot')

Şimdi sembolü (Ticker), veriler arasındaki aralığı (Interval), ilk verinin tarihini ve son verinin tarihini tanımlıyoruz:

Ticker = 'BTC-USD'
Interval = '1d'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

Artık verileri şu şekilde alabiliriz:

DF = yf.download(tickers=Ticker, interval=Interval, start=Date1, end=Date2)

Yukarıdaki yöntemin dışında aşağıdaki yöntem de kullanılabilir:

Interval = '1d'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

Ticker = yf.Ticker('BTC-USD')
DF = Ticker.history(interval=Interval, start=Date1, end=Date2)

Pandas Datareader kütüphanesini aşağıdaki gibi de kullanabilirsiniz:

Ticker = 'BTC-USD'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

DF = pdt.DataReader(Ticker, data_source='yahoo', start=Date1, end=Date2)

Bu şekilde her üç yöntemde de çıktı bir veri çerçevesi olacaktır. Bağlantı hızı veya internet bağlantısının kesilmesi nedeniyle zaman zaman veri almanın zor olabileceğini lütfen unutmayın.

Ortaya çıkan veri çerçevesini görüntülemek için şunu yazıyoruz:

print(DF.head())

Ve aşağıdaki gibi sahip olacağız:

                  Açık Yüksek Düşük Kapatma Ayarı Kapatma Sesi
Tarih
31.12.2014 310.914001 320.192993 310.210999 320.192993 320.192993 13942900
2015-01-01 320.434998 320.434998 314.002991 314.248993 314.248993 8036550
2015-01-02 314.079010 315.838989 313.565002 315.032013 315.032013 7860650
2015-01-03 314.846008 315.149994 281.082001 281.082001 281.082001 33054400
2015-01-04 281.145996 287.230011 257.612000 264.195007 264.195007 55629100

Şimdi son 200 gündeki fiyatın mum grafiğini aşağıdaki gibi çiziyoruz :

mplf.plot(DF.iloc[-200:], type='candle')
plt.show()

Bu sayede diyagram aşağıdaki gibi olacaktır.

Bu şekilde bir mum grafiği çizilir. Artık hacim grafiğini ekleyebiliriz. Ek olarak, 13 günlük ve 55 günlük pencereli iki hareketli ortalama , trendleri ve seviyeleri iyi bir şekilde gösterebilir:

mplf.plot(DF.iloc[-200:], type='candle', mav=(13, 55), volume=True)
plt.show()

Bu durumda aşağıdaki diyagram elde edilecektir.

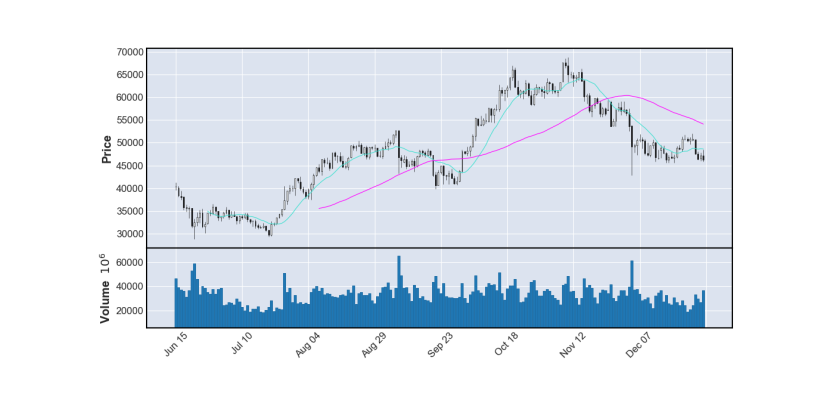
Bu sayede grafiklerin iyi çizimi ve paylaşım davranışı da görülebilmektedir.

Veri ön işleme

Tahminin ilk aşamasında yalnızca Kapat verilerini kullanıyoruz.

Bunun için öncelikle sembolün kapanış fiyatına ilişkin sütunu çıkarıyoruz:

C = DF['Close'].to_numpy()

Daha sonra istenilen değişkenin grafiğini çizeriz:

plt.plot(C, lw=0.7, c='crimson')
plt.title('BTC Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price (USD)')
plt.show()

Yukarıdaki kodun çıktısında aşağıdaki şekli elde edeceğiz.

Grafiğin çizildiğini görüyoruz. Piyasanın üstel yapısından dolayı ilk 700 gündeki fiyat değişiklikleri pek görülmez.

Bu sorunu çözmek için fiyatın logaritmasını alıp grafiği yeniden çiziyoruz:

S = np.log(C)

plt.plot(S, lw=0.7, c='crimson')
plt.title('BTC Price Logrithm')
plt.xlabel('Time (Day)')
plt.ylabel('Log(Price (USD))')
plt.show()

Ve çıktıda aşağıdaki şekle sahip olacağız.

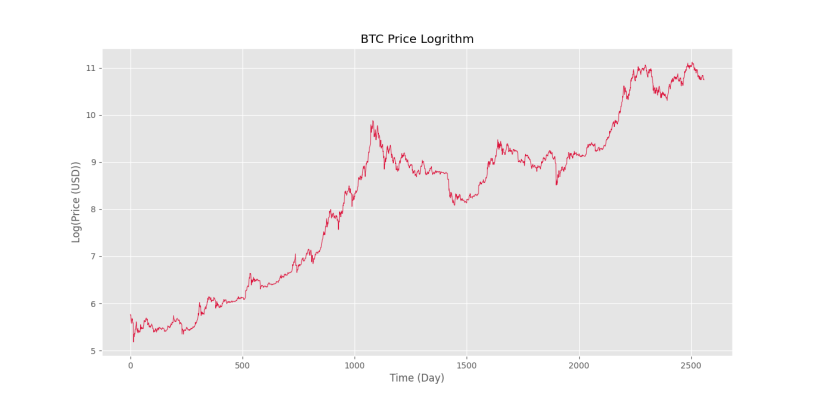
Bu sayede fiyat seviyelerindeki farkın da iyi bir şekilde giderildiğini görüyoruz. Zaman serisinin trendini sabitlemek için farklılaşma, doğrusal trend çıkarma, hareketli ortalama veya Hodrick-Prescott Filtresi gibi yöntemler kullanılabilir.

Şimdi veri kümesini oluşturmak için Gecikme işlevini uyguluyoruz:

def Lag(S:np.ndarray, L:int):
    nD0 = S.size
    nD = nD0 - L
    X = np.zeros((nD, L))
    Y = np.zeros((nD, 1))
    for i in range(nD):
        X[i, :] = S[i:i + L]
        Y[i, 0] = S[i + L]
    return X, Y

Bu işlev aşağıdaki adımları gerçekleştirir:

1. Giriş zaman serisinin boyutu belirlenir.
2. Çıkış verilerinin boyutu belirlenir (serinin başlangıcında L veri için hiçbir x ve y çiftinin oluşturulamayacağı göz önüne alındığında).
3. X ve Y için iki boş dizi oluşturulur.
4. Tüm veriler için X ve Y matrislerinin her satırı başlatılır.
5. Oluşturulan veri seti çıktıya döndürülür.

Bu işlevi kullanarak zaman serisini kullanılabilir bir veri kümesine dönüştürürüz:

nLag = 30
X0, Y0 = Lag(S, nLag)

Artık “eğitim verilerinin” (Eğitim Veri Kümesi) yüzdesini belirleyebilir ve ardından sayılarını hesaplayabiliriz:

sTrain = 0.8
nDtr = int(sTrain * S.size)

Artık verileri iki eğitim ve test veri kümesine ayırabiliriz:

trX0 = X0[:nDtr]
teX0 = X0[nDtr:]
trY0 = Y0[:nDtr]
teY0 = Y0[nDtr:]

Bu şekilde veriler bölünür. Şimdi verinin ölçeğini değiştiriyoruz:

SSX = pp.StandardScaler()
trX = SSX.fit_transform(trX0)
teX = SSX.transform(teX0)

SSY = pp.StandardScaler()
trY = SSY.fit_transform(trY0)
teY = SSY.transform(teY0)

Yalnızca bir hedef niteliğin olduğunu göz önünde bulundurarak hedef diziyi şu şekilde değiştiriyoruz:

trY = trY.reshape(-1)
teY = teY.reshape(-1)

Otokorelasyon modeliyle fiyat tahmini

Şimdi tahminlerde bulunmak için “otoregresif” bir model kullanıyoruz. Bu konu hakkında daha fazla bilgi edinmek için ” Python’da Otoregresif Model – Adım Adım Kılavuz ” makalesine başvurabilirsiniz .

• Python mu yoksa JavaScript mi? Hangi dil daha iyi?

Artık doğrusal bir model oluşturabilir ve onu eğitebiliriz:

Model = lm.LinearRegression()
Model.fit(trX, trY)

Model değerlendirme kriterlerini hesaplamak için modeli ve verileri alarak istenilen kriterleri hesaplayıp çıktıya yazdıracak bir fonksiyonu aşağıdaki gibi tanımlıyoruz:

def RegressionReport(Model, X:np.ndarray, Y:np.ndarray):
    P = Model.predict(X)

    MSE = met.mean_squared_error(Y, P)
    RMSE = MSE**0.5
    NRMSE = 100 * RMSE / (np.max(Y) - np.min(Y))
    MAE = met.mean_absolute_error(Y, P)
    MAPE = 100 * met.mean_absolute_percentage_error(Y, P)
    R2 = 100 * met.r2_score(Y, P)

    print(f'MSE:   {round(MSE, 4)}')
    print(f'RMSE:  {round(RMSE, 4)}')
    print(f'NRMSE: {round(NRMSE, 2)} %')
    print(f'MAE:   {round(MAE, 4)}')
    print(f'MAPE:  {round(MAPE, 2)} %')
    print(f'R2:    {round(R2, 2)} %')

Bu işlev ilk önce modelin verilere ilişkin tahminini alır, ardından sklearn.metrics veya mevcut ilişkileri kullanarak çeşitli ölçümleri hesaplar. Son olarak her kriter yazdırılır.

Şimdi verileri eğitmek ve test etmek için yazılı işlevi çalıştırıyoruz:

print('Model Regression Report on Train Dataset:')
RegressionReport(Model, trX, trY)
print('_'*60)
print('Model Regression Report on Test Dataset:')
RegressionReport(Model, teX, teY)

çıktıda sahip olacağımız şey:

Tren Veri Kümesine İlişkin Model Regresyon Raporu:
MSE: 0,0007
RMSE: 0,0273
NRMSE: %0,85
MAE: 0,0175
MAPE: %8,95
R2: %99,93
____________________________________________________________
Test Veri Kümesine İlişkin Model Regresyon Raporu:
MSE: 0,0008
RMSE: 0,0276
NRMSE: %2,05
MAE: 0,0201
MAPE: %1,06
R2: %99,55

Bu sayede her iki veri setindeki modelin katsayısının birbirine yakın ve uygun olduğunu gözlemliyoruz. Eğitim veri setindeki MAPE kriterinin değerinin test veri setinden 8 kat daha yüksek olduğunu unutmayın, bu ilk bakışta garip gelebilir. Bunun nedeni eğitim veri setinde 0’a yakın değerlerin bulunmasıdır.

Son yıllarda sembol fiyatının yüksek oranda artması nedeniyle veri setinin en alt %20’lik kısmında sayılar ortalamanın üzerindedir ve bu nedenle eğitim veri setinde sıklıkla 0’a yakın değerler mevcuttur. . Ayrıca NRMSE kriterinin değerinde büyük bir fark bulunurken, RMSE’ler arasında büyük bir fark bulunmamaktadır. Bu aynı zamanda veri aralığındaki farklılıktan da kaynaklanmaktadır. Verilerin üst %80’i daha geniş bir aralık (5’ten 10’a kadar) içerirken, alttaki %20’si daha küçük bir aralık (9’dan 11’e kadar) içerir. Bu nedenle eğitim veri setindeki RMSE’nin 2,5 katı normaldir.

Bu kriterleri incelemek için ” Python‘da Regresyon Değerlendirme Kriterleri İncelemesi – Uygulama + Kodlar ” makalesine başvurabilirsiniz .

Diyagram çizin

Şimdi eğitim ve test verileri için orijinal zaman serisini ve model tahminini çiziyoruz:

trP = Model.predict(trX)
teP = Model.predict(teX)

plt.plot(trY, lw=0.9, c='crimson', label='Target Values')
plt.plot(trP, lw=0.9, c='teal', label='Predicted Values')
plt.title('Model Result on Train Dataset')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.legend()
plt.show()

plt.plot(teY, lw=0.9, c='crimson', label='Target Values')
plt.plot(teP, lw=0.9, c='teal', label='Predicted Values')
plt.title('Model Result on Test Dataset')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.legend()
plt.show()

Yukarıdaki kodun çıktısında aşağıdaki iki grafik elde edilmektedir.

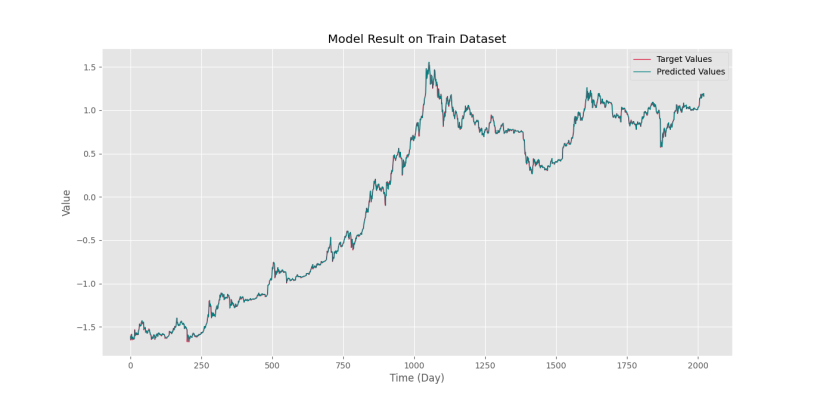
İkinci diyagram aşağıdaki resimde verilmiştir.

Bu sayede model tahmininin gerçek verilere çok yakın olduğunu görebiliyoruz. Ancak mesele şu ki, model tahminde biraz geç kaldı. Aslında model, son günün fiyatını yarın için bir tahmin olarak kullanmaya çalışır (geçmiş fiyatları kullanarak hafif bir iyileşme ile).

Modelin geçmiş günlere ait ağırlığını görmek için şu şekilde hareket ediyoruz:

W = Model.coef_
print(f'W:\n{W}')

sahip olacağımız şey:

[+3.58563953e-02 -1.96077112e-02 -1.20056042e-02
 -1.88671111e-02 +2.53669946e-02 +5.83798116e-03
 +6.07673595e-03 -1.94466868e-02 +2.97395294e-02
 -5.50333940e-02 -2.67256590e-02 +3.38254901e-02
 -3.09856605e-02 +4.98994631e-02 -6.81061580e-03
 -8.07773671e-04 +4.84668241e-03 -8.51348645e-03
 +5.97168971e-04 -4.92384255e-02 +8.77800917e-02
 -2.10080279e-02 +2.11319993e-02 -8.05356204e-02
 +2.68525320e-02 +1.56674539e-02 +2.31580583e-03
 -1.30531651e-02 +4.58633245e-02 +9.70581002e-01]

Bu sayede giriş verilerinin son günü için 0,97’lik bir ağırlık belirlendiğini görüyoruz, bu da modelin son günü kullanma eğiliminin yüksek olduğunu gösteriyor. Aslında model, bir sonraki güne ait değişiklikleri hesaplamaya ve bunu son günün fiyatına eklemeye çalışır.

Modelin davranışını dengelemek için Ridge ve Lasso ve Elastic Net modellerini kullanabiliriz. Tahminin ölçeklendirildiğini unutmayın. Tahmin ölçeğini verinin ana ölçeğine dönüştürmek için önce Ters Dönüşüm yapılmalı, ardından Üstel fonksiyon uygulanmalıdır:

trP0 = np.exp( SSY.inverse_transform( trP.reshape( (-1, 1) ) ) )
teP0 = np.exp( SSY.inverse_transform( teP.reshape( (-1, 1) ) ) )

Modelin davranışını iyileştirmek için nLag değeri optimize edilebilir. Bu amaçla Kısmi Otokorelasyon Fonksiyonunu (PACF) çizebiliriz:

tsaplt.plot_pacf(S, lags=500, c='teal', lw=0.4, markersize=1)
plt.xlabel('Lags (Days)')
plt.ylabel('Pearson Correlation Coefficient')
plt.show()

Aşağıdaki diyagram elde edilir.

Bu şekilde aşağıdaki gecikmelerin de anlamlı bir ilişki gösterdiğini gözlemliyoruz:

$$\text{Gecikmeler}=1,4,5,14,15,29,195$$

Bu nedenle, 30 başlangıç ​​gecikmesinden yalnızca 6 gecikmenin anlamlı olduğunu gözlemliyoruz. Bu şekilde yalnızca 29 başlangıç ​​gecikmesi kullanılabilir ve nispeten iyi bir doğruluk elde edilebilir. 1 ile 29 arasındaki tüm gecikmeler yerine yalnızca 1, 4, 5, 14, 15 ve 29 gecikmelerinin seçici olarak kullanılabileceğini unutmayın.

Python’da fiyat tahmininin özeti

Bu yazıda Python’da bir sonraki günün fiyatını tahmin etmek için doğrusal regresyon kullandık.

Daha fazla okumak için aşağıdakileri kontrol edebilirsiniz:

1. Veri kümesine seçici olarak gecikme eklemek için Gecikme işlevini değiştirin.
2. Giriş özelliklerinde önemsiz gecikmelerin varlığı hangi sorunlara neden olur?
3. Eğitim için verinin %80’ini zaman serisinin başından seçmek yerine, tüm zaman serisinin içinden rastgele seçmek mümkün müdür?
4. Zaman serisi ön işleme bölümünde trendi çıkarmak ve sonuçları karşılaştırmak için bahsedilen yöntemlerden birini kullanın.
5. KNN, SVM ve MLP modellerini veri kümesi üzerinde eğitin ve sonuçları karşılaştırın.
6. Ertesi günkü fiyat değerini tahmin etmek yerine artış, azalış ve nötr olmak üzere üç kategoride değişimin yönünü tahmin etmek istiyorsak kodu nasıl değiştirmeliyiz?