Python’da Zaman Serisi Tahmin Projesi

esmail

1 year ago

Zaman Serisi konularında “Tahmin” için bir altlık oluşturmak çok önemlidir . Tahminler yapmak için bir temel, araştırmacıya diğer modellerin belirli bir problem üzerinde ne kadar iyi çalıştığına dair bir fikir verir. Bu kılavuzda, bir zaman serisi veri setindeki çeşitli modellerin temel performans düzeyini hesaplamak için kullanılabilecek istikrarlı bir tahmin modelinin nasıl geliştirileceği pratik bir örnekle öğretilmektedir. Python’da zaman serisi tahmini projesi konusunda aşağıdaki konular ele alınmıştır.

Zaman serisi tahmin problemleri için temel verimlilik hesaplamasının önemi
Python’da sıfırdan kararlı bir model nasıl geliştirilir?
İstikrarlı bir modelden kaynaklanan tahmini değerlendirme ve bunu performansta bir temel oluşturmak için kullanma yöntemi

Tahmin etkinliğinin temeli

Temel, performansı tahmin etmede bir karşılaştırma noktası sağlar. Model taban çizgisinden daha düşük performans elde ederse, atılmalı veya geliştirilmelidir. Temel verimliliği hesaplamak için bir tahmin oluşturmak için kullanılan yöntemin uygulanması kolay ve probleme özel olmalıdır. Araştırmacı, tahmin probleminin performans temelini belirlemeden önce, bir “Otomatik Test Çerçevesi” geliştirmelidir. Bu çerçeve aşağıdakileri içerir:

Kullanıcının modeli eğitmek ve değerlendirmek için kullanmak istediği veri seti.
Kullanıcının yöntemin performansını tahmin etmek için kullanacağı yeniden örnekleme yöntemi (örneğin, eğitim ve test veri kümeleri).
Birinin tahminleri değerlendirmek için kullanma eğiliminde olduğu performans ölçüsü (örneğin, Ortalama Karesel Hata ) .

Temel tahmin yapmak için iyi bir yöntemin üç özelliği şunlardır:

Basitlik: Yöntem, az miktarda eğitim verisi gerektirir veya hiç veri veya zeka gerektirmez.
Hızlı: Uygulanması hızlı ve tahminler yapmak için hesaplama açısından basit bir yöntem.
Tekrarlanabilir: Yöntem deterministik olmalıdır, yani aynı girdi verildiğinde beklenen çıktıyı üretecektir.

Temel verimlilik oluşturmak için yaygın bir algoritma “Kalıcılık Algoritması” dır.

mana algoritması

Denetimli makine öğrenimi için en yaygın temel yöntem “sıfır kuralı” algoritmasıdır. Bu algoritma, sınıflandırmada çoğunluk sınıfını veya regresyon analizinde ortalama çıktıyı belirler. Bu algoritma zaman serileri için kullanılabilir; Ancak algoritma, zaman serisi veri setindeki seri korelasyon yapısını dikkate almaz.

Zaman serisi veri kümeleriyle kullanım için eşdeğer bir yöntem Kalıcılık Algoritmasıdır. Mana algoritması, bir sonraki zaman adımında (t+1) beklenen çıktıyı tahmin etmek için önceki zaman adımındaki (t-1) değeri kullanır. Bu, yukarıda belirtilen üç koşulun temel tahmin için karşılanmasını sağlar. Aşağıda, bir Mana modelinin nasıl geliştirileceği incelenmekte ve bu model, tek değişkenli bir zaman serisi problemi için temel performans oluşturmak için kullanılmaktadır . İlk olarak, şampuan satış veri seti üzerinde bir vaka çalışması yapılacaktır.

Şampuan satış veri seti

“Şampuan Satış Veri Kümesi”, son üç yıldaki şampuan satışlarını gösterir. Numuneler satış sayısı ile ilgilidir ve içerisinde 36 adet gözlem (örnek) bulunmaktadır. Orijinal veri seti Makridakis, Wheelwright ve Hyndman (1998) içindir. Aşağıda, söz konusu veri setinin başlık dahil ilk beş satırına ait örnekler verilmiştir.

"Ay", "Satış"
"1-01", 266.0
"1-02", 145.9
"1-03", 183.1
"1-04", 119.3
"1-05", 180.3

Aşağıdaki resim, tüm veri kümesinin bir grafiğidir (izleyiciler bu veri kümesini indirebilir ve hakkında daha fazla bilgi edinebilir).

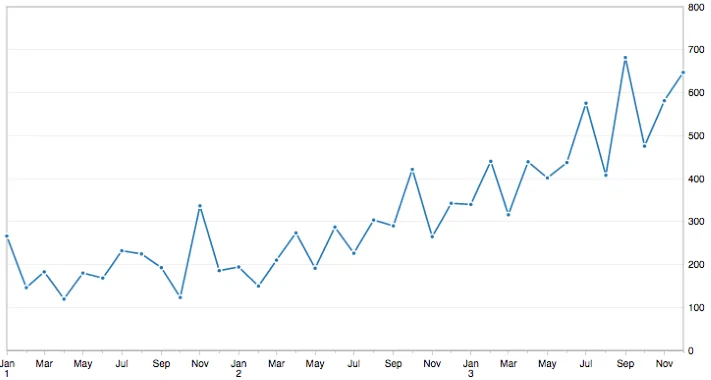
Veri seti, artan bir eğilim ve muhtemelen mevsimsel bileşenler göstermektedir. Veri setinin [ + ] indirilmesi ve “shampoo-sales.csv” dosya adıyla geçerli çalışma klasörüne yerleştirilmesi önerilir . Aşağıdaki kod parçacığı, şampuan satışları veri kümesini yükler ve zaman serisini çizer.

from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
 
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
 
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
series.plot()
pyplot.show()

Yukarıdaki kodu çalıştırarak, çıktı diyagramı aşağıdaki gibi elde edilir:

Python ve Mana algoritmasında zaman serisi tahmin projesi

Bir Mana modeli Python’da kolayca uygulanabilir. Aşağıda, uygulama çalışması beş adıma bölünmüştür.

Tek değişkenli bir veri setini denetimli bir öğrenme problemine dönüştürme
Otomatik bir test çerçevesi için test ve eğitim veri kümeleri oluşturma
Mana modeli tanımı
Üssün verimliliğini tahmin etme ve açıklama
Tüm örneği gözden geçirin ve çıktı diyagramını çizin

1. Adım: Denetimli öğrenme problemini tanımlama

İlk adım, veri kümesini yüklemek ve bir post-render oluşturmaktır. Bu şekilde, t-1 zamanındaki gözleme dayalı olarak, t+1 zamanındaki gözlem tahmin edilir.

# Create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
print(dataframe.head(5))

Yukarıdaki kod parçacığı, veri kümesini oluşturur ve yeni veri kümesinin ilk beş satırını yazdırır. İlk gözlemden önce herhangi bir gözlem olmadığı için ilk satırın (indeks 0) atlandığı görülmektedir. Denetimli makine öğrenimi açısından, t-1 sütunu bir giriş değişkeni veya x’tir ve t+1 sütunu bir çıkış değişkeni veya y’dir.

t-1 t+1
0 NaN 266.0
1 266,0 145,9
2 145,9 183,1
3 183,1 119,3
4 119,3 180,3

Adım 2: setlerin eğitimi ve test edilmesi

Bir sonraki adım, veri setini iki kategoriye ayırmaktır: “Eğit” ve “Test”. İlk gözlemlerin %66’sı eğitim için ve geri kalan %34’ü test için kullanılır. Bölümleme sırasında NaN değerleri içeren satırların göz ardı edilmemesine dikkat edilmelidir. Bu durumda herhangi bir eğitim gerekli değildir. Eğitim ve test setlerinin her biri daha sonra girdi ve çıktı değişkenlerine bölünür.

# split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]

3. Adım: Mana algoritması

Bir temel algoritma, girdi olarak sağlanan değeri döndüren bir işlev olarak tanımlanabilir. Örneğin, t-1 değeri 266.0 sağlanırsa, bu tahmin olarak döndürülür; meydana gelen beklenen veya gerçek değer 145.9 iken (sonraki veri setindeki ilk kullanılabilir satırdan alınmıştır).

# persistence model
def model_persistence(x):
	return x

4. Adım: Tahmin edin ve değerlendirin

Şimdi, model test veri seti üzerinde değerlendirilir. Bu, “İleri Yürü” doğrulama yöntemi kullanılarak yapılır. Modeli eğitmeye veya yeniden eğitmeye gerek yoktur. Bu nedenle test veri setinde zaman adımlarına dayalı olarak tek tek tahmin yapılmaktadır. Eğitim veri kümesindeki her zaman adımı için tahminler yapıldıktan sonra, bu tahminler beklenen değerler ve Ortalama Karesel Hata (MSE) puanı ile hesaplanır.

# walk-forward validation
predictions = list()
for x in test_X:
	yhat = model_persistence(x)
	predictions.append(yhat)
test_score = mean_squared_error(test_y, predictions)
print('Test MSE: %.3f' % test_score)

Bu makalede, test veri setinde hata 177730’dan fazladır.

Adım 5: Tam örnek

Son olarak, eğitim veri setini ve test veri setinden gerçek değerlerden farklı tahminleri gösteren bir grafik çizilir. Mana modelinin tahmin tablosundan 1 adımlı modelin gerçeğin arkasında olduğu açıkça anlaşılmaktadır. Aydan aya satış rakamlarında artan bir trend ve satış rakamlarında gürültü var, bu da Mana yönteminin sınırlamalarını vurguluyor.

Tam bir örnek aşağıda verilmiştir.

from pandas import read_csv
from pandas import datetime
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
from sklearn.metrics import mean_squared_error
 
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
 
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# Create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
print(dataframe.head(5))
 
# split into train and test sets
X = dataframe.values
train_size = int(len(X) * 0.66)
train, test = X[1:train_size], X[train_size:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]
 
# persistence model
def model_persistence(x):
	return x
 
# walk-forward validation
predictions = list()
for x in test_X:
	yhat = model_persistence(x)
	predictions.append(yhat)
test_score = mean_squared_error(test_y, predictions)
print('Test MSE: %.3f' % test_score)
 
# plot predictions and expected results
pyplot.plot(train_y)
pyplot.plot([None for i in train_y] + [x for x in test_y])
pyplot.plot([None for i in train_y] + [x for x in predictions])
pyplot.show()

Bu yazıda şampuan satma problemi için baştan aşağı sunulan bir Mana modeli incelenmiştir. Mana’nın algoritması basittir ve genellikle “Saf Tahmin” olarak adlandırılır. Bu model, uygulandığı zaman serisi problemi hakkında herhangi bir varsayımda bulunmaz. Bu, anlaşılmasını kolaylaştırır ve hızlı bir şekilde uygulanmasını ve değerlendirilmesini sağlar.

Bir makine öğrenimi öngörücüsü olarak bu model, önemli iyileştirmeler de görebilir. Bu yararlıdır çünkü bu fikirler, özellik mühendisliği sürecinde girdi özellikleri veya montaj sürecinde birleştirilebilecek basit bir model olabilir.

Çözüm

Bu makalede, Python programlama dili kullanılarak zaman serisi tahmin problemleri için temel bir yöntemin nasıl oluşturulacağı öğretilmiştir. Ayrıca taban yöntemi oluşturmanın önemi, Python’da Mana algoritmasının sıfırdan nasıl uygulanacağı ve Mana algoritmasında tahmin değerlendirme yöntemi ve bunu temel olarak kullanma konuları incelenmiştir.

Python ile penetrasyon testi nasıl yapılır?