Python’da K-means kümeleme algoritmasını uygulama

K-Means, en yaygın kullanılan veri kümeleme algoritmalarından biridir. K-ortalamalarda, sabit eylemleri tekrarlayarak ve Norm, Ortalama ve Argmin gibi fonksiyonları kullanarak, her bir küme için yüksek doğruluk ve düşük eylemsizliğe sahip merkezler bulmak mümkündür .

K-means algoritmasındaki amaç, bir kümedeki noktalar (veriler) arasındaki mesafeyi en aza indirmektir. K-means, bir kümeye bir nokta atamak için mesafelerin hesaplandığı merkez tabanlı veya mesafe tabanlı bir algoritmadır. K-ortalamalarda, her kümenin bir merkezi vardır. K-means algoritmasının temel amacı, karşılık gelen kümenin merkezi ile noktalar arasındaki mesafelerin toplamını en aza indirmektir.

K-means algoritmasını uygulama adımları nelerdir?

Genel olarak, K-means algoritmasını uygulama adımları aşağıdaki gibidir:

1. Küme sayısının belirlenmesi (K)
2. Küme merkezlerinin koordinatları olarak verilerden K rasgele sayı seçme
3. Tüm noktaların (verilerin) en yakın küme merkezine atanması
4. Her bir kümenin verilerinin ağırlıklı ortalamasını merkez olarak seçmek
5. Durdurma kriteri sağlanana kadar 3. ve 4. adımları tekrarlayın.

K-means algoritması için durdurma kriterleri nelerdir?

Temel olarak, K-means algoritmasının yineleme döngüsünü durdurmak için üç durdurma kriteri kullanılabilir. Bu üç kriter aşağıda sıralanmıştır:

1. Yeni oluşturulan kümelerin merkezleri değişmez.
2. Noktalar (veriler) aynı kümede kalır ve veriler için küme üyeliği değişmez.
3. Tekrar sayısı, maksimum (belirtilen) tekrar sayısına ulaşır.

K-means algoritmasının matematiksel ilişkisi nedir?

Bu algoritma matematiksel dilde şu şekilde olacaktır:

$$C_J=MeAN\left(A_J\right(T–1\left)\right),T⩾1$$

$$A_J\left(T\right)=\{X_{\mathrm{Ben}}\mid X_{\mathrm{Ben}}\in X,J=\underset{\text{J}}{ARGM\mathrm{Ben}N}(NÖRM(X_{\mathrm{Ben}}–C_J(T\left)\right)\left)\right\}$$

Makalenin devamında K-means nedir, Python’da bu algoritmanın implementasyonu anlatılmaktadır. Ancak bundan önce, bu alanla ilgilenenler için bir dizi ders dışı veri madenciliği ve makine öğrenimi kursu tanıtıldı.

• Python ile penetrasyon testi nasıl yapılır?

K-means’ın Python’da uygulanması

Makalenin bu bölümünde K-means nedir, Python’da  algoritmasını uygulama eğitimi adım adım sunulmaktadır. İlk adım, kullanılan kütüphaneleri çağırmaktır.

Python’da K-means algoritmasını uygulamak için kitaplıkları çağırma

K-means algoritmasının Python’da uygulanması, numpy ve Matplotlib kitaplıklarını kullanır, bu nedenle programlama ortamına girmeli ve bu kitaplıkları çağırmalısınız:

import numpy as np
import matplotlib.pyplot as plt

Bir sonraki adımda, K-ortalamalarını çalıştırmak için sentetik veriler tanımlanmalıdır. Bu çalışma bu nedir makalesinin bu bölümünün devamında yapılmıştır.

Python’da K-means algoritmasını uygulamak için yapay veriler oluşturma

Python’da K-means algoritmasını uygulamak için gerekli kütüphaneler çağrıldıktan sonra, şu algoritmasının gerçeklenmesinden elde edilen sonuçların gerçek değerlerle karşılaştırılabilmesi için küme merkezleri belirlenmiş bir veri seti oluşturulmalıdır.

şu belirli küme merkezleriyle sentetik veri üretmeye yönelik kodlar aşağıdaki gibidir:

def CreateDataset(Cs, nD, S):
    nC = len(Cs)
    N = nD * nC
    X = np.zeros((N, 2))
    for i in range(0, nD):
        for j in range(0, nC):
            X[nC*i + j, 0] = Cs[j, 0] + np.random.randn() / S
            X[nC*i + j, 1] = Cs[j, 1] + np.random.randn() / S
    return X

Yukarıdaki kodlarda oluşturulan CreateDataset fonksiyonunda, her bir giriş merkezi etrafında rastgele bir dizi nD verisi oluşturulmakta ve çıktıda döndürülmektedir.

Yapay veri oluşturma işlevini çağırma

CreateDataset işlevini çağırmak aşağıdaki gibidir:

# Centers of Synthetic Data
Cs = np.array([[-0.5, +1.0], [+1.6, -0.1],
                [-0.9, -1.7], [-2.9, +2.3],
                [+0.7, +2.2], [-2.2, +0.3]])
nD = 200 # Count of Data in Each Cluster
S = 2.5

X = CreateDataset(Cs, nD, S)

Yukarıdaki kodda, nD, Cs ve S dahil olmak üzere CreateDataset işlevinin giriş parametreleri tanımlanır ve başlatılır. Daha sonra CreateDataset fonksiyonu çağrılır ve tanımlanan değişkenler bu fonksiyona girdi olarak iletilir. İşlevi yürüttükten sonra, gerekli veriler X dizisinde saklanacaktır.

Oluşturulan verilerin görselleştirilmesi

Oluşturulan verileri görüntülemek ve görselleştirmek için veriler bir dağılım grafiği olarak çizilebilir:

plt.style.use('ggplot')
plt.scatter(X[:, 0], X[:, 1], c = 'k', s = 9, label = 'Data')
plt.scatter(Cs[:,0], Cs[:, 1], c = 'r', s = 100, label = 'Center', marker = '*')
plt.title('Scatter Plot of Data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()

Yukarıdaki kodlarda plt.scatter komutunun iki kez kullanıldığına dikkat edilmelidir. plt.scatter’ın ilk çağrısında X matris verilerinin dağılımı, ikinci çağrısında ise kümelerin merkezleri çizilir. Bu makalede, Python’da K-means algoritmasını uygulamak için iki boyutlu veriler kullanılmıştır. Bu çalışma, hesaplamaları basitleştirmek ve verileri grafikte gösterme imkanı sağlamak amacıyla yapılmıştır. CeateDataset işlevinde X boyutları değiştirilerek daha yüksek boyutlu veriler oluşturulabilir. Yukarıdaki kodların dağıtım şeması çıktıda şu şekilde yazdırılır:

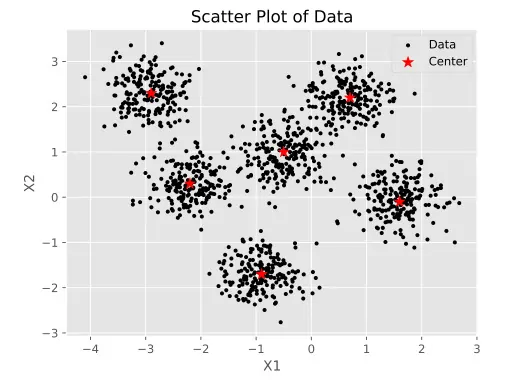
Küme sayısının ve merkezlerinin belirlenmesi

nClusters = 6

Centers = np.random.uniform(-2, +2, (nClusters, 2)) # Initializing Centers Posotions

Yukarıdaki kodlarda, rastgele küme merkezlerini belirlemek için alt ve üst aralıkların değiştirilebileceğine dikkat edilmelidir. Üretilen verilerin iki boyutlu olduğu düşünüldüğünde kümelerin merkezleri de iki boyutlu bir ortamda konumlanacaktır.

Her veriyi bir kümeye atamak için bir işlev oluşturun

Bir sonraki adımda, kümelerin merkezlerinin koordinatlarını ve içindeki noktaları alan bir fonksiyon oluşturulmalıdır.$$X$$, her veri en yakın kümeye atanır ve son olarak her kümedeki bir veri dizisi döndürülür. Bu fonksiyon aşağıdaki gibi tanımlanır:

def GetClusters(Centers, nClusters, X):

Her kümenin verilerini depolamak için bir liste oluşturun

Şimdi, nClusters kadar boş liste içeren bir liste oluşturulmalıdır, böylece daha sonra her veri o kümeye karşılık gelen listeye eklenir:

def GetClusters(Centers, nClusters, X):
    Clusters = []
    for i in range(0, nClusters):
        Clusters.append([])

Yukarıdaki kodların çıktısında Cluster listesi aşağıdaki gibi olacaktır.

$$C\mathrm{ben}\mathrm{sen}STeRS=\left[\right[],[],\dots ,[\left]\right]$$

Merkezden herhangi bir noktanın uzaklığını hesaplayın

Şimdi her veri için olmalı$$X_{\mathrm{Ben}}$$, her merkezden uzaklık$$C_J$$hesaplandı. Bunu yapmak için, önce tüm veriler üzerinde bir döngü oluşturun ve ardından her bir merkezin uzaklığını eklemek için boş bir dizi oluşturun.$$X_{\mathrm{Ben}}$$tanımlanmış

Bundan sonra tüm küme merkezleri için uzaklık$$X_{\mathrm{Ben}}$$e kadar$$C_J$$hesaplanmış Bu şeyler aşağıdaki kodlarda yapılır:

for xi in X:
        d = np.zeros(nClusters)
        for j in range(0, nClusters):
            cj = Centers[j]
            dij = xi - cj
            d[j] = np.linalg.norm(dij)

Yukarıdaki kodlarda iki vektör çıkarılarak$$X_{\mathrm{Ben}}$$Ve$$C_J$$birbirinden almak$$D_{(}\mathrm{Ben},J)$$L2 – Norm değerinin Öklid mesafesini ifade edeceği ortaya çıktı . Varsayılan olarak, norm işlevi L2 yöntemini kullanır . Tabii ihtiyaç halinde başka yöntemler de kullanılabilir. Artık verilmesi gerekiyor$$X_{\mathrm{Ben}}$$en yakın küme merkezine karşılık gelen listeye eklendi:

        a = np.argmin(d) # Arg of Nearest Center
        Clusters[a].append(xi) # Appending Xi to Nearest Centers List

Bu sayede istenilen fonksiyon artık tamamlanmış olur ve gerekli fonksiyonu yerine getirir.

Küme listelerini dizilere dönüştürün

Sonunda, kullanımlarını kolaylaştırmak için Kümelerdeki listeleri dizilere dönüştürmek daha iyidir:

def GetClusters(Centers, nClusters, X):
    Clusters = []
    for i in range(0, nClusters):
        Clusters.append([])
    for xi in X:
        d = np.zeros(nClusters)
        for j in range(0, nClusters):
            cj = Centers[j]
            dij = xi - cj
            d[j] = np.linalg.norm(dij)
        a = np.argmin(d) # Arg of Nearest Center
        Clusters[a].append(xi) # Appending Xi to Nearest Centers List
    for i in range(0, nClusters):
        Clusters[i] = np.array(Clusters[i])
    return Clusters

Artık oluşturulan işlevi programın ana metninde kullanabilirsiniz:

nClusters = 6

Centers = np.random.uniform(-2, +2, (nClusters, 2)) # Initializing Centers Posotions
Clusters = GetClusters(Centers, nClusters, X)

Python’da K-means algoritmasının tekrarlanan 3. ve 4. adımlarının uygulanması

“K-means nedir” yazısında bu noktaya kadar, K-means algoritmasının 1. ve 2. adımları tamamlanmış ve Python’da gerçeklenmiştir, şimdi 3. ve 4. adımların tekrarını gerçekleştirmek için, oluşturma ihtiyacı vardır. bir döngü:

nIter = 20

for i in range (0, nIter):

Öncelikle küme merkezlerinin koordinatları her adımda güncellenmelidir. Bu işlem için aşağıdaki gibi bir fonksiyon tanımlanmalıdır:

def UpdateCenters(Centers, Clusters, nClusters):

Şimdi, her bir küme için karşılık gelen merkez, o kümenin ortalama noktalarına yerleştirilmelidir:

def UpdateCenters(Centers, Clusters, nClusters):
    for i in range(0, nClusters):
        Centers[i] = np.mean(Clusters[i], axis = 0)

Bu nedenle değerler np.mean işlevi kullanılarak güncellenir. Bu aşamada önemli olan nokta eksen değeridir. Bu durumlarda eksen değeri sıfır olmalıdır ki ortalama alma işlemi satır başına değil, sütun başına yapılmalıdır. Bu bölümde ortaya çıkabilecek problem bir küme ile ilgili dizinin boş olmasıdır.

Böyle bir durumda ortalama değer hiçbir$$\frac{0}{0}$$gelecek, bu da programın uygulanmasını aksatacaktır. Bu nedenle, ilgili dizi boş değilse güncelleme işleminin gerçekleştirilebilmesi için bir koşul ayarlanmalıdır:

def UpdateCenters(Centers, Clusters, nClusters):
    for i in range(0, nClusters):
        Centers[i] = np.mean(Clusters[i], axis = 0)
        if np.size(Clusters[i]) != 0: # if Array is not Empty
            Centers[i] = np.mean(Clusters[i], axis = 0)
    return Centers

Bu şekilde merkezlerin güncellenmesi için gerekli fonksiyon oluşturulmuş olur. Şimdi oluşturulan döngünün tamamlanması gerekiyor:

nIter = 20

for _ in range (0, nIter):
    Centers = UpdateCenters(Centers, Clusters, nClusters)
    Clusters = GetClusters(Centers, nClusters, X)

Bu nedenle, K-means algoritmasının uygulaması Python’da yapılmıştır ve K-means algoritması doğru çalışacaktır.

K-means algoritmasının uygulanan sonuçlarının gerçek küme merkezleri ile karşılaştırılması

Adımlar tamamlandıktan sonra K-Means algoritması sonucu ortaya çıkan merkezlerin koordinatlarını belirlenen merkezlerle karşılaştırmak mümkündür.

plt.scatter(Cs[:,0], Cs[:,1], label='Target Centers', marker = '*', s = 80, c = 'r')
plt.scatter(Centers[:,0], Centers[:,1],
            label='Centers Found by K-Means', marker = 'x', s = 60, c = 'k')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()

Yukarıdaki kodları çalıştırdıktan sonra çıktı görüntüsü aşağıdaki gibi olacaktır:

K-ortalama algoritma adımlarının görsel gösterimi

Çözüm

Bu yazıda öncelikle k-means algoritması nedir sorusuna cevap verilmiş ardından K-means algoritmasının Python‘da implementasyonu adım adım ve olabildiğince basit bir şekilde sunulmuştur. Bu uygulamada bunlara yönelik yapay üretim verileri ve küme merkezleri belirlenmiştir. Daha sonra K-ortalamaları gerçekleştirmek için gerekli kodlar ve fonksiyonlar oluşturulmuş ve bu algoritma üretilen veriler üzerinde çalıştırılarak sonuçları kümeler için belirlenen merkezler ile karşılaştırılmıştır.